Any matter that has a temperature higher than its surroundings emits radiation at various frequencies. The total amount of radiation and the distribution of the emitted wavelengths depend almost entirely on the temperature of the body and are not characteristics of the material itself. For an idealised black body that absorbs all radiation that falls onto it, this relationship between temperature and wavelength of maximum emission is completely precise. Many astronomical bodies, such as stars, can be considered to be almost perfect black bodies, so we can apply all the characteristics of a black body to them. Let's have a look at the radiation of black bodies at different temperatures:

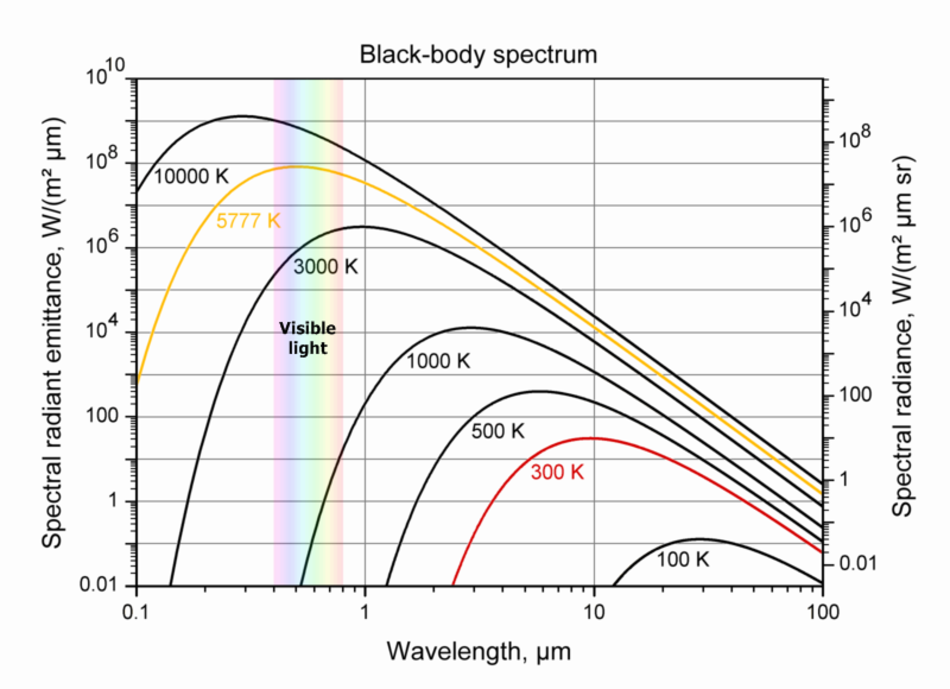Wien's displacement law showing the relationship between emitted radiation and the temperature of a black body, Source: Wikimedia Commons user Sch, adapted by Sun.org

We can see examples of the spectrum of emitted radiation for seven bodies at different temperatures, ranging from 100 degrees Kelvin to 10000 degrees Kelvin. Please note that this diagram is logarithmic. That means that the difference from one scale point to the next along each axis is a factor of 10! The range of visible light is indicated with the colours of the rainbow between 0.4 and 0.8 µm.

There are two important things to notice:

1. The higher the temperature, the more intense is the emitted radiation. The formula to express this is the Stefan-Boltzmann law:

   F = σ x T⁴

   with F being the radiation flux in W/m², σ being a physical constant, the so called Stefan-Bolzmann Constant, and T being the temperature of the object. Note that the flux increases with the fourth power of the temperature. A body with a surface temperature of 2000 degrees Kelvin radiates 16 times more energy than a body with a temperature of 1000 degrees Kelvin.


2. With increasing temperatures the wavelength of maximum emission shifts from lower energy, long wavelengths to higher energy, short wavelengths. This phenomenon is described by the Wien's displacement law, named after a German physicist with the remarkable name of Wilhelm Carl Werner Otto Fritz Franz Wien. A body at room temperature (about 300 degrees Kelvin) emits radiation mainly around a wavelength of 10 µm, which is infrared. Our sun, with its surface temperature of about 5777 degrees Kelvin, emits most of its radiation at about 0.5 µm (or 500 nm), which is visible light.

A red dwarf with a surface temperature of 3000 K emits much more light towards the red end of the visible spectrum, hence it appears red. The hot stars appear blue since they emit a bigger part of their radiation in blue than they do in red. Technically they have their peak radiation in the ultraviolet wavelengths that humans can't detect. And since in addition our eyes are not very good at detecting a violet colour (the shortest wavelength we can see) these stars appear blue to us.

It is important to understand the exact radiation pattern of celestial bodies and then scan the sky at all wavelengths. This way we can detect bodies within a wide range of temperatures. A brown dwarf for example has a temperature of 1000 degrees Kelvin and can best be observed in the infrared at about 3 µm; at wavelengths of visible light its radiation is about 100 000 to one million times weaker.